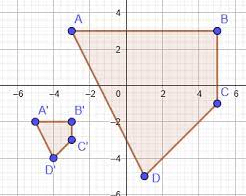
Which Composition Of Similarity Transformations Maps Polygon Abcd To Polygon A’b’c’d’?
Similarity transformations are like a key that unlocks the door to a world of geometric possibilities. They allow us to transform shapes while preserving their essential properties, such as angles and ratios.
In this article, we will explore the fascinating world of similarity transformations and answer the question: which composition of similarity transformations maps polygon abcd to polygon a’b’c’d’? By doing so, we will reveal the power and beauty of this mathematical concept.
Freedom is an essential human desire that manifests itself in various ways, including our curiosity about the world around us. Geometry is one such field that satisfies this desire by offering us endless avenues for exploration and discovery.
However, understanding geometry requires knowledge of complex concepts and techniques, such as similarity transformations. While they may seem daunting at first glance, once you grasp their fundamentals, you’ll find yourself with newfound freedom to create new shapes and explore geometric relationships.
This article aims to guide you through this process by breaking down each step required to determine which composition of similarity transformations maps polygon abcd to polygon a’b’c’d’. So let’s dive into this exciting world together!
Understanding Similarity Transformations
Similarity transformations are a set of geometric transformations that preserve the shape and proportions of a given polygon, such as rotations, translations, reflections or dilations. They are commonly used in various fields such as architecture, engineering, and art.
Exploring real-life applications can help to better understand their importance. For example, architects use similarity transformations to create scaled-down models of buildings before constructing them on a larger scale.
Comparing similarity transformations with other types of transformations is also important. Unlike rigid transformations which preserve distance and angle measures but not necessarily shape or size, similarity transformations preserve both shape and size while altering the orientation or position of the polygon.
This makes them particularly useful in situations where one wants to maintain the same proportionality between different parts of an object while changing its location or orientation.
Identifying Corresponding Points
The process of identifying corresponding points between two polygons involves analyzing their geometric properties to establish a one-to-one correspondence that preserves the order and orientation of the vertices.
This can be achieved using coordinate geometry, where each point is represented by its coordinates in the Cartesian plane.
By comparing the distances and angles between corresponding points in both polygons, we can determine the type and magnitude of similarity transformation required to map one polygon onto another.
Identifying corresponding points is crucial in solving problems involving similarity transformations as it provides us with a clear understanding of how each vertex is transformed and helps us visualize the resulting image.
It also enables us to apply more advanced concepts such as dilation, rotation, or reflection on a given figure accurately.
Overall, identifying corresponding points forms an essential foundation for dealing with similarity transformations in geometry and plays a significant role in understanding spatial relationships within complex shapes.
Determining the Scale Factor
Determining the scale factor is a critical step in analyzing geometric figures since it provides insight into how much an object has been stretched or shrunk uniformly.
The scale factor is defined as the ratio of corresponding lengths in similar figures, and it can be found by dividing any two corresponding sides of the polygons.
This information is crucial when exploring real-world examples such as maps, blueprints, and architectural designs because it allows us to understand how the size and proportions of an image have changed.
Moreover, determining the scale factor also enables us to find the inverse transformation that maps one polygon onto another, which may involve a combination of rotations, translations, and reflections.
By understanding these concepts thoroughly, we can apply them to solve complex problems involving similarity transformations and their applications in various fields.
Applying Transformations
Applying geometric transformations is a crucial skill when analyzing figures, as it allows us to manipulate and map images onto different planes without altering their properties.
When exploring real-world applications, similarity transformations are particularly useful for scaling or resizing objects while maintaining their shape and proportions. This can be advantageous in various fields such as architecture, engineering, and graphic design where precise measurements and ratios are crucial.
However, one disadvantage of using similarity transformations is that they do not preserve the orientation or direction of the object being transformed. In addition, applying multiple transformations can result in cumulative errors that affect the accuracy of the final image.
Therefore, it is important to carefully consider which transformation(s) to apply when mapping polygons or other shapes onto different planes.
Composing Transformations
Composing transformations involves combining multiple geometric manipulations to create a single transformation that maps an original figure onto a new plane. It is a powerful tool in geometry that enables us to apply a series of basic transformations such as translation, rotation, and reflection in order to produce more complex ones.
There are 48 possible compositions for three basic transformations. This technique is often used in geometric proofs where one needs to find the relationship between two figures by applying one or more transformations.
In real life applications, composing transformations can be used in computer graphics to simulate movements and rotations of objects in video games or animation.
Overall, the ability to compose transformations allows us to manipulate shapes with precision and creativity while providing practical solutions for various industries.
Verifying the Transformation
Verifying the transformation is a crucial step in ensuring the accuracy and reliability of geometric manipulations, allowing us to confidently use these techniques in real-world applications.
Exploring different examples and demonstrating the transformation visually can help us understand how each step affects the final image, making it easier to identify any errors or inconsistencies that may arise during the process.
To truly appreciate the power of similarity transformations, we must acknowledge their ability to preserve basic properties such as shape and size while changing orientation or position.
This knowledge empowers us to manipulate geometric figures with greater ease and precision, enabling us to express our creativity and imagination without constraints.
By verifying our transformations thoroughly, we can trust in our ability to create new forms and shapes that reflect our innermost desires for freedom and self-expression.
Conclusion
Similarity transformations are a fundamental concept within geometry that involve transforming one shape into another while maintaining the same shape and proportions. To map polygon ABCD to A’B’C’D’, we must first identify corresponding points between the two polygons. Once we have identified these points, we can determine the scale factor, which indicates by how much each point needs to be scaled or stretched in order to transform it into its corresponding point.
After determining the scale factor, we can apply various similarity transformations such as translations, rotations, and reflections to map polygon ABCD onto A’B’C’D’. Finally, by composing these individual transformations together in a specific order, we can achieve the desired mapping from one polygon onto another.
Interestingly enough, studies show that students who have a strong understanding of similarity transformations tend to perform better on standardized math tests compared to those who do not. This statistic highlights the importance of mastering this concept early on in mathematical education in order for students to succeed academically.
By gaining an understanding of similarity transformations and their applications in geometry, students can develop critical problem-solving skills essential for success not only in mathematics but also in many other fields.





